Einfachheit der Struktur - Grundlagen

Die strukturelle Betrachtung von Software-Systemen ist den meisten Softwareschaffenden am vertrautesten. Intuitiv werden Software-Systeme bevorzugt in Strukturen gesehen, d. h. in Elementen einer bestimmten Art und ihren Relationen. Diese Denkweise ist zudem aus einigen häufig genutzten Diagrammtypen gut vertraut. Folgerichtig beziehen sich zahlreiche Entwurfsprinzipien auf die Güte von Strukturen, und nicht selten bedeutet "Güte" vor allem eines: Die Struktur soll so einfach wie möglich sein. Doch was ist eigentlich eine "einfache" Struktur?

Hätten wir es nur mit einer einzigen Struktur-Ebene zu tun, wäre die Antwort leicht: Eine Struktur wäre dann einfacher als eine andere, wenn sie aus weniger Elementen und Relationen bestünde. Wir hatten jedoch bereits im Rahmen der Beschreibung des allgemeinen Modells für Software-Systeme ausgeführt, dass Software-Systeme hierarchisch aufgebaut sind somit mehrere Struktur-Ebenen aufweisen. Wir sehen uns daher vor die Aufgabe gestellt, die Grundlagen einer strukturellen Betrachtungsweise unter Berücksichtigung mehrerer Ebenen zu erarbeiten.
 

1. Elemente und Relationen auf verschiedenen Struktur-Ebenen

Strukturen werden aus Elementen aufgebaut, die in Relation zueinander stehen. Auf verschiedenen System-Ebenen finden wir verschiedenartige Elemente vor. Wir hatten in einem weitgehend technologieunabhängigen allgemeinen Modell für Software-Systeme u. a. die Ebenen System, Subsysteme, Pakete, Typen, Funktionen, Konstrollstrukturen und die Ebene der Repräsentation unterschieden. Auf jeder dieser Ebenen stellt ein Element eine Gruppierung von Elementen der nächst tieferen Ebene dar.

2. Grundidee: Reduktion von Elementen und Relationen  

Die naheliegende Grundidee zur Vereinfachung einer Struktur besteht darin, die Zahl der Elemente und Relationen so gering wie möglich zu gestalten. Dies könnte dazu verleiten, die Elemente einer Ebene so weit als möglich zu verschmelzen: Die Verschmelzung reduziert zugleich die Anzahl der Elemente als auch der Relationen. Bedauerlicherweise ignoriert diese Vorgehensweise zwei wesentliche Aspekte:

• Ursprung der Relationen: Der Ursprung aller Relationen eines Software-Systems, gleich auf welcher Ebene sie betrachtet werden, liegt im Bereich der Funktionen und Daten.
• Aktuale vs. potentielle Struktur: Die Einfachheit einer Struktur resultiert nicht nur aus der Anzahl der tatsächlich vorhandenen (aktualen) Relationen, sondern auch aus der Anzahl der möglichen (potentiellen) Relationen.

3. Funktionen und Daten als Ursprung aller Relationen

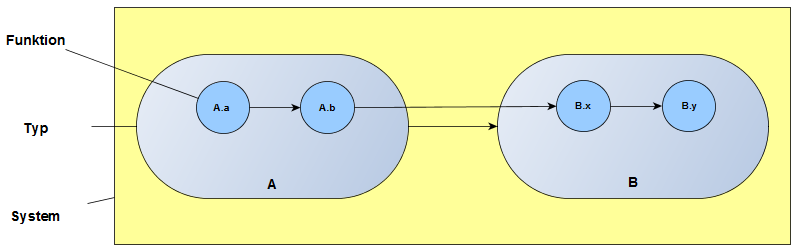
Der Ursprung aller Relationen auf den verschiedenen Struktur-Ebenen eines Software-Systems liegt im Bereich der Funktionen und Daten. Betrachten wir zur Erläuterung dieses Sachverhalts die verschiedenen Ebenen des allgemeinen Modells für Software-Systeme, wobei wir uns hier auf die logische Dimension konzentrieren und die physische ausblenden. (Das Gesamtmodell wird im Abschnitt "3.3.1. Allgemeine Systemhierarchie" im Artikel über das allgemeine Modell für Software-Systeme beschrieben.)

Die Abbildung zeigt eine Relation zwischen einer Funktion links und einer Funktion oder einem Daten-Objekt rechts. Diese Relation wird auf die höheren Ebenen lediglich projiziert. Bestünde sie nicht, so bestünde auch keine Relation zwischen Typ A und Typ B, zwischen Paket X und Paket Y sowie zwischen Subsystem S und Subsystem T. Selbst wenn sich rein syntaktisch eine Relation zwischen den Elementen höherer Ebenen herstellen ließe, die nicht auf einer Nutzung einer Funktion oder eines Daten-Objekts basiert (wie z. B. ein ungenutzter Import auf Typ-Ebene), so könnte diese syntaktische Relation konzeptionell ignoriert werden, da sie problemlos entfernt werden kann, ohne dass sich das Systemverhalten ändert. Ich werde eine Relation auf der Ebene der Funktionen und Daten im Folgenden kurz als funktionale Relation bezeichnen.

Bei der Projektion einer funktionalen Relation auf eine höhere Ebene kommt es häufig zu einer scheinbaren Vereinfachung. Denn mehrere funktionale Relationen zwischen zwei Typen werden auf der Typ-Ebene auf eine Relation reduziert. Mehrere Typ-Relationen zwischen zwei Paketen werden auf Paket-Ebene auf eine Relation reduziert usw. Mit dieser scheinbaren Vereinfachung geht ein Informationsverlust auf der höheren Ebene einher. Dieser Informationsverlust ändert aber nichts am tatsächlichen Umfang der weiterhin vorhandenen funktionalen Relationen.

4. Aktuale vs. potentielle Struktur

Die aktuale Struktur einer Ebene wird durch die tatsächlich vorhandenen Elemente auf dieser Ebene sowie die tatsächlich vorhandenen Relationen dieser Elemente bestimmt. Da die scheinbare Vereinfachung der Relationen auf höheren Ebenen letztlich nur auf einem Informationsverlust beruht, ergibt sich die Komplexität der aktualen Gesamtstruktur im Wesentlichen aus den tatsächlich vorhandenen funktionalen Relationen. Ich bezeichne diese Komplexität im Folgenden als aktuale Strukturkomplexität.

Die aktuale Strukturkomplexität ist jedoch nicht gleich der Strukturkomplexität des Gesamtsystems. Diese wird wesentlich mitbestimmt durch die Anzahl der möglichen funktionalen Relationen, die ich im Folgenden als potentielle Strukturkomplexität bezeichne. Während sich die aktuale Strukturkomplexität ausschließlich aus den tatsächlich realisierten funktionalen Relationen ergibt und von höheren Struktur-Ebenen völlig unabhängig ist, gilt dies für die potentielle Strukturkomplexität keineswegs. Dies hängt damit zusammen, dass der Zugriff auf Funktionen und Daten durch höhere Struktur-Ebenen eingeschränkt werden kann. 

Denn höhere Struktur-Ebenen sind keine reinen Gruppierungen ihrer enthaltenen Elemente, sondern können auch die Sichtbarkeit ihrer Elemente nach außen hin einschränken. Ist eine Funktion oder ein Daten-Objekt außerhalb eines solchen Struktur-Elements nicht sichtbar, so steht es außerhalb dieses Elements auch nicht für die Bildung funktionaler Relationen zur Verfügung. Daraus resultiert eine Reduktion der potentiellen Strukturkomplexität des Gesamtsystems.

Wir können nun die Strukturkomplexität wie folgt definieren:

C_S = a * C_a + (C_p - C_a) + b * |E|

mit

• C_S = Strukturkomplexität
• C_a = aktuale Strukturkomplexität = Anzahl der aktualen funktionalen Relationen
• C_p = potentielle Strukturkomplexität = Anzahl der potentiellen funktionalen Relationen
• |E| = Anzahl der Funktionen und Daten-Objekte
  
• a = Gewichtungsfaktor der aktualen gegenüber der potentiellen Struktur 
• b = Gewichtungsfaktor für die Anzahl der Elemente

Wir können für die Zwecke dieser Betrachtung die Faktoren a und b ignorieren, da wir hier nicht auf eine konkrete Metrik hinarbeiten, sondern lediglich die Zusammenhänge verstehen wollen, die eine Struktur einfacher machen als eine andere. Der Faktor a wäre so zu justieren, dass die tatsächlich vorhandenen Relationen stärker in die Rechnung einfließen als die bloß potentiellen. Der Faktor b drückt nicht nur aus, dass ein Struktur-Element für sich genommen eine andere Bedeutung hat als eine Relation, sondern repräsentiert auch einen Aufschlag für die durchschnittliche Komplexität der Funktionen hinsichtlich der tieferen Ebenen der Kontrollstrukturen und der Repräsentation.

In der Formel wird C_a von C_p abgezogen, da die mit a gewichtete aktuale Strukturkomplexität bereits in die Summe eingeflossen ist und nicht ein weiteres Mal einfließen soll. Für die weitere Betrachtung werde ich a = 1 setzen und die Anzahl der Elemente ignorieren, also b = 0 setzen. Dies reicht aus, um das für diesen Artikel Wesentliche zu erfassen. Es ergibt sich die folgende vereinfachte Formel:

C_S = C_p

Die angestellte Betrachtung liefert uns nun das Handwerkszeug, um zu verstehen, warum triviale Verschmelzungen auf einzelnen Struktur-Ebenen nicht den gewünschten Effekt einer Vereinfachung haben, sondern im Gegenteil die Komplexität erhöhen können.

5. Beispiel einer kontraproduktiven "Vereinfachung"

Wir betrachten ein System aus zwei Typen A und B mit jeweils zwei Funktionen, die als A.a, A.b, B.x und B.y bezeichnet werden. Das aktuale System sieht auf den drei Ebenen System, Typ und Funktion wie folgt aus:

Das System weist insgesamt drei tatsächlich realisierte funktionale Relationen auf, nämlich A.a -> A.b, B.x -> B.y sowie A.b -> B.x. Wir können zusätzlich davon ausgehen, dass die Funktionen A.a, A.b sowie B.y nur innerhalb ihrer jeweiligen Typen sichtbar sind, während B.x auch außerhalb von B sichtbar ist. Somit ergeben sich insgesamt sechs potentielle funktionale Relationen, je zwei innerhalb der Typen A und B sowie die zwei Relationen von A.a und A.b zum öffentlichen Element B.x. Daraus ergibt sich die folgende Strukturkomplexität:

C_S = C_p = 6

Wir möchten dieses System nun "vereinfachen", indem wir die Typen A und B zum Typ A' verschmelzen. Dies führt zu folgendem System:

Die Hoffnung dieser Vereinfachung ist, dass nun auf der Typ-Ebene nur noch ein Element und keine Relation mehr existiert, was nach einer Vereinfachung klingt. Da die aktuale Strukturkomplexität jedoch auf der Basis der funktionalen Relationen ermittelt werden muss, ist sie unverändert gleich drei. Schlimmer noch, durch die Zusammenführung in einem Typen sind nun alle Funktionen für alle anderen Funktionen sichtbar geworden, was zu 4 * 3 = 12 potentiellen funktionalen Relationen führt. Somit liegt die Strukturkomplexität nun bei

C_S = C_p = 12

Die Steigerung wächst mit der Zahl der Elemente quadratisch an, so dass die Verschmelzung größerer Elemente ggf. zu einer erheblichen Komplexitätssteigerung führt.

6. Fazit 

Die oben angestellten Überlegungen haben zu einigen interessanten Erkenntnissen geführt:

• Betrachtet man ausschließlich das tatsächlich realisierte System, so spielt die Aufteilung der Funktionen und Daten-Objekte auf die diversen Gruppierungen höherer Ebenen (wie Typen, Pakete, Subsysteme usw.) keine Rolle für die beobachtete strukturelle Komplexität (=aktuale Strukturkomplexität) des Systems.
• Die Strukturierung dieser höheren Ebenen, d. h. die Aufteilung der Funktionen und Daten-Objekte auf Typen, Pakete, Subsysteme usw. ist jedoch sehr bedeutsam für die Größe des strukturellen Lösungsraums (= potentielle Strukturkomplexität) eines Systems und damit auch für die tatsächlichen Ressourcen, die im Umgang mit dem System benötigt werden.
• In einem völlig unstrukturierten System, in dem alle Funktionen und Daten-Objekte in potentieller Relation zueinander stehen, ergibt sich die Gesamtkomplexität als |E| * (|E| - 1), sie steigt also quadratisch zur Anzahl der Funktionen und Daten-Objekte. Wir haben für die Zwecke dieses Artikels die Anzahl der Elemente sowie ihre durchschnittliche Komplexität ignoriert und können die Formel daher in dieser Weise vereinfachen. An dieser Stelle sollte aber klar geworden sein, dass die angestrebte strukturelle Vereinfachung insbesondere durch Einschränkung des Zugriffs auf Funktionen und Daten-Objekte erreicht werden kann und dass zu diesem Zweck die entsprechenden Mittel höherer Struktur-Ebenen eingesetzt werden können.